ORM
- Check The Facts
Are Of The Right Arity
This step is designed
to fix incorrect (either too long, or too short) fact types. Here we
decide if higher arity facts should be split
Every fact type
bigger than a BINARY is examined - in this step we are collecting evidence
to support the splitting of the fact into smaller parts. We apply a
number of tests to the fact type and if all the tests fail, we accept
that the fact type is ok, otherwise it is split up.
(a) Functional
Dependence (and a little common sense)
Fact types should
be split if parts of them are unrelated to the attributes attached to
them.
TutGroup(Tnum) in House(Hname) collectedwalkathonamount Money(Dollarcount)
-is a true ternary,
as the amount collected depends on the house designation and the tutor
group number (i.e. dollar count is functionally dependant upon
tut group-house).
Person(name) hasHeight Length(cm) atAge YearCount(num) inClass YearLevel(YrCode)
- is not a quaternary,
as the attributes height and YearLevel are dependent on the Person-YearCount
combination, and have nothing to do with each other (ie. they are functionally
independent) - better expressed as 2 ternaries.
Person(name) enrolledin Degree(Dcode) obtained Rating(rcode) in Subject(Scode)
- again is not a
quaternary, as the degree enrolled does not functionally determine the
results in a subject
general:
given a significant fact table, the fact is splittable if a column is
functionally dependent on only some (but not all) of the other columns
(b) Minimum Key
Length
simple rule:
for an n-ary fact, if there exists a uniqueness constraint spanning
n-2 roles or less, then the fact type is of incorrect arity and MUST
BE SPLIT.
eg: a ternary fact
type with a single (3-2) role uniqueness constraint is in fact 2 binaries
eg: a quaternary
with a 2 (4-2) role uniqueness is probably a ternary (or may be lower
still) and a binary
case k of
n : definitely unsplittable;
n -1 : probably unsplittable;
n -2 : definitely splittable
end; {case}
REMEMBER
- every fact type with an arity > 2 is immediately suspect - the minimum
key length determines the likelihood of splittability
The above fact type
is obviously incorrect as there is a uniqueness constraint on Person
(minimum key length = 1, fact length = 3 - therefore definitely splittable
(c) Projection
- Join Check
This allows you
(so long as you have a significant fact table population) to
decide if high (> arity 3) facts can be expressed as a lower arity without
information loss (or phantom creation)
table := signifigantInstanceCollection;
repeat
split table in an untried way by projection;
perform Equijoin;
splittable := resulttable = originalTable
until splittable or everySplitTried
Please note, this
step is exhaustive (as the arity of the fact increases, the number
of different possible splits also increases), but is VITAL that all
possible splits are checked. A high (>2) arity fact is GUILTY OF
SPLITTABILITY until proven otherwise.
eg1: Company Project Article
C1 P1 A1
C1 P1 A2
C2 P1 A2
C2 P2 A2
we form 3 - arity
2 tables (Company+Project; Company+article; Project+Article) and project
the relevant populations (as sets of tuples) - then attempt to equijoin
various combinations to re-form the original
eg2: Dealer Manufacturer VehicleType
Smith Ford Car
Smith Ford Truck
Smith Holden Car
Smith Holden Truck
Jones Ford Car
Ensure that when
splitting, you have representative data - else the equijoin could convince
you that the fact type is the wron arity when more data may convince
you otherwise - this example highlights the problem
eg3: Supplier ServiceType Customer
S1 T1 C1
S1 T2 C2
S2 T1 C1
S2 T1 C3
S2 T3 C3
S3 T1 C3
(s-t X t-c) X (s-c) reforms base population
therefore really
have 3 binaries (each with many to many uniquenes constraints) - this
example is extremely nasty (much harder than you would get on an exam)
(d) Look at nests
carefully
As an extension
of minimum key length splittability testing, all nested fact
types should be scrutinised carefully, ensuring that the objectified
relationship suffers a whole role (or many to many) uniqueness
constraint. If this is not the case, then splittability is definite!
Further Constraints
ORM
- Further Constraints
Add Entity Type,
Cardinality, Mandatory Role, Occurrence Frequency and Subtype Constraints
Populations - defining
a Sub-Type
The population of
an entity is the set of values (instances) that are associated with
it.
eg.
In the single binary : Student studies Subject

pop(student) = pop(studies)
= {a,b} say
pop(subj) = pop(studiedby)
= {ipt,eng,ch,bio}, say
Convention:
{} is used for string (text labels)
[] is used for numeric data
Consider an extension
to the above universe:
pop(student) < > pop (plays)
pop(student) = pop(plays) U pop(studies)
= {a,e,c,d} U {a,b}
= {a,b,c,d,e}
(a) Entity Type
Constraints
pop(entity) = pop(r1)
U pop(r2) U .... pop(rn)
the population of
an entity equals the union of the populations of all the roles associated
with the entity
On a CS diagram,
if a specific (small) ordered set of values apply to an entity, list
them
eg: {label1, label2, label3...}
or [value1, value2, value3...]
eg. {hot, cold} [-70 degrees..+70 degrees] is a reasonable 'fuzzy' boundary
if the list is exhaustive,
LEAVE IT OUT (ie. list only if reasonable). Providing such DOMAIN
SPECIFICATIONS often relies on 'insiders knowledge' of the Universe,
or access to such expertise.
(b) Cardinality
Constraints - fortunately less common.
- used to indicate
the number of values an entity may have
- used when enumeration
is unnecessary (or values unknown)
- if used in place
of entity type constraints INFORMATION LOSS occurs (to say there are
6 houses is weaker than saying the six houses are named 'Windsor,
Kearney, Reidy.....)
place a numeral
next to the entity being constrained
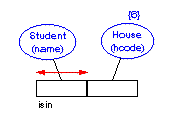
note this
annotation indicates that the maximum number of houses is six, but that
their codes are not yet defined (as was the case when the student database
was being written back in 1992, prior to house naming).
(c) Mandatory And
Optional Roles
It is important
to distinguish required knowledge (often by referring to the real world).
eg. a persons gender
- in the real world everyone has exactly one, but in an employment application
form for a firm that believes in gender equity, it may not need to be
filled in.
Generally, if a
role (R) is optional for some entity E, then it will always be true
that:
pop(R) <= pop(E) (ie. the population of a role is a subset
of an entities popn)
For a MANDATORY
ROLE, however:
pop(R) = pop(E) (ie. the population of a role equals the
entities popn)
(ie. all entities play the role)
pop(r2) is a subset
of pop(E1)
pop(r1) = pop(E1)
pop(E1) = pop(r1)
= pop(r2) = pop(r3). That means that E1 plays ALLof the roles
r1..r3
It is stated in
the above diagram that:
E1 MUST play roles r1 and r2; MAY play role r3; MUST
play at least ONE of roles r4, r5 and r6 (and may even play
all three)
The above schema
fragment states that:
E1 plays r1 at least once; E1 plays r2 at most once; E1
plays r3 exactly once
Finally, the absence
of a role dot = OP on a table design presence of a role dot = MA on
a table design
The above schema
fragment states:
any amount of money shown must be a COST PRICE, SELLING PRICE or BOTH;
Each item has EXACTLY ONE cp and sp; derived fact types (profit) must
be shown as optional
(d) Occurrence
Frequency Constraints
basically - placing
a number above a particular role to indicate mandatory participation
in that fact type.
All E1s play r1
n times (or no times at all); E1's play r2 EXACTLY m times (or they
are not in the database); E4's play r3's converse exactly p times (as
the only reason they exist is participation in the fact type)
be warned - some
combinations of occurrence frequency constraints with uniqueness and
mandatory role constraints are REDUNDANT
Sub-ranges can also
be quoted as Occurrence frequencies (ie. n..m means participates in
the fact type between n and m times)
Further reading
on this issue is in Chapter 26, pages 11 to 18
(e) Sub-Typing
Often, we have seen
the case where fact types relate to only a certain subset of entity
instances (eg. in ANCEGYPT, there are attributes of a RULER, and more
general attributes of people - grouping them together causes NULLS)
A NULL could mean:
- does not exist
(and we know it) - complete knowledge
- is not recorded
(and never is) - complete knowledge
- not known if
the instance exists - incomplete knowledge
- not known if
the fact type exists - incomplete knowledge
consider:
People have exactly one gender, students study courses, lecturers receive
exactly one salary.
Clearly, there are
attributes that relate to sub-populations of the person entity - to
include them as attributes of that entity would create excessive NULLS
in the tables generated.
consider
Article Code Colour Price Size Neck
Dress 134-6 Red 50.00 14 ?
Dress 214-5 Yellow 45.00 12 ?
Skirt 712-0 Red 34.95 12 ?
Shirt 615-8 White 50.00 ? 90
Shirt 547-2 White 25.00 ? 85
where ?=NULL=NEVER TO BE RECORDED
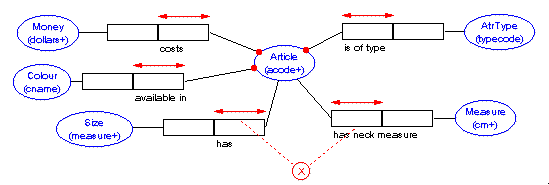
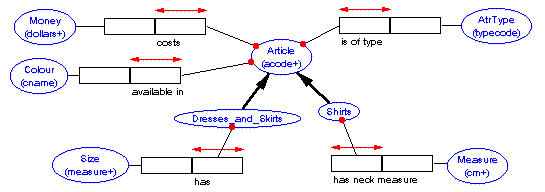
NOTE:
the schema without subtyping has OPTIONAL roles - meaning possible NULLS
in the resulting tables, where as the sub-typed schema has only MANDATORY
roles (ie. no NULLS)
SUPERTYPE: contains general entity attributes, and sub-type
categorisation information (so you can tell what
sub-type is what)
SUB-TYPE: contains the name of the sub-type and fact types
that relate ONLY to that subtype
Each of the sub-types
INHERIT all of the general characteristics of the SUPERTYPE.
How to Spot A Sub-Type
Situation
- when there are
a lot of OPTIONAL roles on a schema, sub-typing is suggested
- when you can
see (easily) that there are attributes that belong to discrete, possibly
disjoint sets of entity instances
consider:
Name Kind CarsChased Age KgMeatEaten
Fido Dog 25 3 8
Leonard Iguana ? 12 3
Fluff cat ? 2 4
Gerald Hippo ? 23 ?
Nip Dog 0 10 6
All animals have
a name, kind and age. Clearly, we have a group of carnivores, and another
of vegetarians, of the carnivores, we have car-chasers and non-car-chasers.
The Sub-type has
a sub-type. In this case, the fact type describing what sub-type they
belong to needs to be MANY to MANY - as some instances belong to 2 subtypes.


