The central datatype for all relational systems is the TABLE. They behave like containers for your data.

Forming relationally acceptable tables 'in their best form' is the aim of this section of the course.

Normalisation

A Conceptual Schema consists of a set of fully normalised relations - that is fact types in elementary form. As part of the process of conceptualising a UoD, each elementary relation is scrutinised, instantiated and (for the most part) as good as they get.

'Good' database design balances a number of things - the number of NULLS is balanced against the number of tables in the resulting relational schema (sub-typing, as you know, can eliminate the need for nulls).

A CSD, while free of redundancy, may not always lead to an efficient table design (particularly if commonly required 'facts' need to be recreated from many disparate elementary facts). A database designer may choose (after conceptual analysis) to include columns that are redundant in order that certain operations are faster. This choice (called controlled redundancy) comes with enormous risk - update anomalies and referential integrity checks become very complicated (but not un-manageable) under such schemes.

Field typing, although explicit as reference modes on a conceptual schema, may need interpreting based how the implementation is to proceed. Numbers (6.5 as an example instance) could be stored as a real number (which occupies 6-12 bytes of memory) or text (1 byte per character = 3 bytes in this example). The choice bottom-lines on what the values are going to be used for. Certainly, if numerical quantities are required for mathematical calculation, then they should be stored as numbers. If, on the other hand no calculation is required on that numeric field, then storage as text may be justified - ordering, search and retrieval are just as rapid for a fraction of the memory cost.

Optimal Normal Form

Part of the process of conceptualisation is KEY recognition. Each relation instance is distinct from every other relation instance by way enforcement of the uniqueness constraint placed on that relation (during step 4 of ORM). It is appropriate to use the key of the relation to describe (in part) 'what the fact is about' (i.e. it's context).

When deciding what fact types should be grouped into which tables, it is reasonable to expect that relations that are about the same thing should be grouped together. Similarly, fact types that are keyed differently are clearly about different things and belong in separate tables.

Un-Normalised relations involve putting all fields in the one table. Clearly this is inefficient and inappropriate for a relational system in most cases. Incidently, this is the way the vast majority of non-relational database products store their data. Traditionally, Normalisation (First Normal Form up to 5NF) was employed in table design, successively refining tables, splitting and testing until the desired result was obtained - this is time consuming, prone to error and mis-interpretation.

For a given Conceptual Schema, several relational schemas (table designs) may be suggested. The Optimal Normal Form Algorithm (Nijssen & Halpin) aims to provide a simple, safe and efficient table design for a given conceptual schema. These designs have no repeating fields, no redundancy or update problems as each fact is stored only once, and a minimum number of tables to achieve this.

Using ONF, each fact type is mapped into only one table, with the roles sometimes mapping into column names. Since the fact type maps onto a single table, the uniqueness constraints of that fact type become the 'primary' keys for that table. Other uniqueness constraints provide secondary keys, sub-set and equality constraints become foreign keys which lace each of the tables together.

One problem inherited from a number of flavours of SQL (Oracle, Paradox, Access to name a few) is the distinction of a primary key for a table. The name implies that one key (the nominated primary) is more important than other uniqueness constraints (including foreign keys) - this is simply nonsense. The total uniqueness picture is as important as each individual key in defining the behaviour of data stored within the tables. Unfortunately, a number of the key conditions found in the real world are difficult to implement, depending on the SQL flavour chosen.

---

The Optimal Normal Form Algorithm

What follows is a simple method of conceptual-relational mapping. Simple and compound keys are explained as follows:

Simple Keys span a single role box; Compound/Composite Keys span more than one role box

(a) Group fact types with simple keys attached to a common object type into the same table. The primary key for this table is the simple key that was the basis of the group

Notice, the uniqueness constraint that is common for both fact types becomes the primary key for the resulting relation.

Nested fact types provide cases to apply the same rule as each attribute of the nested object has a simple (and common) key, therefore the attributes belong together as they are about the same thing

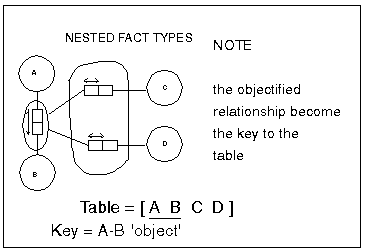
This picture becomes a little clouded in flattened form - look for 'object uniqueness' in groups of high arity facts as these may also be combined into single tables

Constraints spanning fact types either provide secondary keys, or form the basis for foreign keys. Notice that each of the displayed fact types share a simple key (hence the single table), with the inter-fact type constraint also in place.

(b) For each fact type without a simple key, create a separate table. Select the shortest key of the fact type as the primary key for that table

(c) For each fact type remaining, create a separate table. Use the key of the fact type as the primary key of the table.

When the fact type is a 1:1 (i.e. it has two simple keys) where one of the simple keys is common with a collection of other fact types). Such a situation calls for a little common sense and a decision as to whether the fact type belongs with the others or is about something else. A balance between the number of tables and the storage efficiency is called for here. Either way, the fact type will cause a secondary key to exist.

Sub-types present table designers with decisions - put up with nulls in order that a small number of tables is obtained OR increase the number of tables (each sub-type can be its own table) with no nulls.

When deciding on names for table fields, use either the role or the attached entity or some combination to ensure the name is meaningful.

The Data Dictionary

An often overlooked step in table design is the object type listing (otherwise known as the Data Dictionary). Prudent decisions regarding field types can make databases easier to manipulate, be efficient in terms of storage space and to a degree more flexible.

It is suggested that a list of every field, along with the suggested data types be compiled. The aim is minimise the number of different types used and standardise data types across related fields to ensure UNION COMPATIBILITY. This list will greatly simplify the process of table creation during implementation, and will allow some complex inter-field operations later.

As has been suggested, choice of numeric field types may not be efficient in terms of the related storage space. This is particularly so in those cases where mathematical computation is unlikely. The saving in storage space, particularly in large systems can be enormous, without the loss of performance or flexibility.