Algorithms
and Lazarus
Structural
Elements: SELECTION
Decision-making is used all the time - in system terms
we call this decision-making selection. Computers can evaluate whether
something is true or false very efficiently and this TRUE/FALSE outcome
is the basic for boolean logic - we use this to conditionally execute
code: If this is so, then do this, else do this other thing.
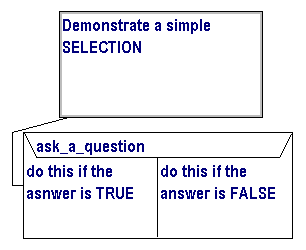
Decisions are relatively easy to verbalise - sometimes however taking
these tests and writing them as legal selections is complex. The computer
is only as smart as the programmed instructions running it and we can
get computer systems to do really crazy things depending on the questions
we get them to evaluate.
Simple BINARY BRANCHING (ask a question and do one thing otherwise do another)
is achieved using an IF THEN ELSE statement. Binary branching is the most
common form of decision making your systems will use. When written correctly
they can be the most efficient way to get something done.
IF [the drink is too warm]
THEN [add ice and drink]
ELSE [drink]
The first part of the selection is the question - in a binary branch
it is typically something that can be answered as yes or no (TRUE/FALSE).
After the question (or test) we have alternative actions. It is obvious
that the "add ice and drink" alternative is performed if the answer to
the test is TRUE. Similarly the "drink" alternative is the one performed
if the test fails (that is the drink is NOT too warm).
In the example above, what is less obvious is the TRUE option is actually
a sequence of 2 simpler steps (add ice and then drink) - it is equally
obvious that the order of the steps in the sequence is important as there
is not much point adding the ice after having drunk the drink.
What may not be obvious here is that regardless of whether the drink is too warm or just right, it is drunk .. logic would suggest that it is not conditionally executed at all, but is done after deciding whether ice is needed:
IF [the drink is too warm]
THEN [add ice];
[drink]
Selections can easily be included in other selections (called nesting)
and the decision logic can get quite complex:
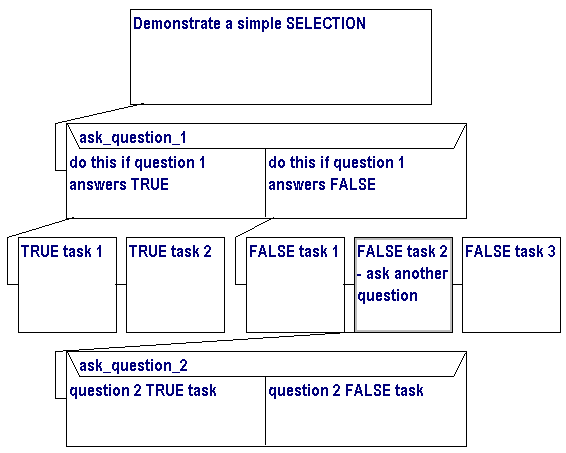
In the above example, we can see a simple selection (question 1) and
a sequence of 2 tasks leading from a TRUE response. From the FALSE response
of question 1 we have a sequence of 3 tasks (one being to ask another
question). The instruction order of this algorithm is not as clear in
this form (a structured design chart).
A flowchart simplifies the SAME algorithm:
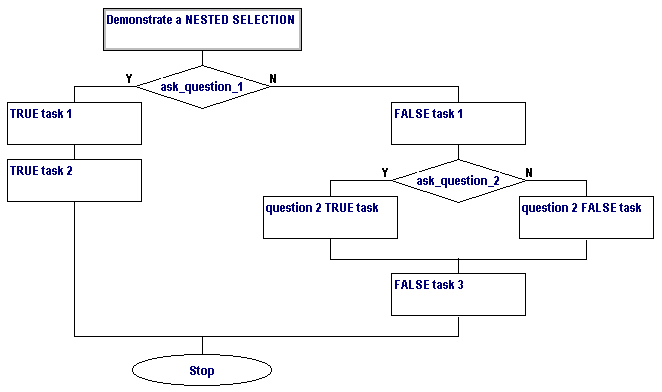
In both diagrams, it is obvious that NOT ALL of the code is executed
- the answers to the questions determine which instructions are run.
In this section of the course, you are encouraged to adopt SOME form
of graphic organiser (SDC or FLOWCHART) for describing parts of your code.
Although this might seem counter-productive, it will aid you in eliminating
LOGICAL ERRORS which are otherwise the most difficult to
identify and rectify in poorly structured programs. Unfortunately there
is no (IWHO) symbolic representation that is great for prepresenting visual
systems yet so we make do with bits-and pieces of other methods.
Experience has shown that the WORST thing a student can do when presented
with a problem is to go and write code before planning. Planning is MUCH
MORE IMPORTANT in visual systems as the multitude of named objects and
built-ins can complicate an otherwise simple-looking task and cause it
to fail.
Multiple selections in Lazarus are catered for by either nested IF..THEN..ELSE
statements or CASE statements.
Consider the following algorithms for dealing with the navigation in
a simplified game:
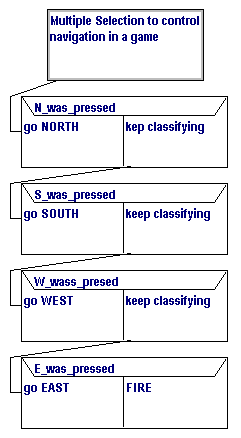
nested |
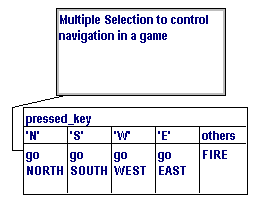
multiple selection |
Both algorithms work, one is more efficient than the other - consider
best and WORSE-case scenarios.
- In the nested example the smallest number of questions asked
is ONE (if an 'N' is pressed). The largest number of questions asked
is FOUR (if none of 'N','S','W' or 'E' are pressed)
- In the multiple selection case, the SMALLEST and LARGEST number of
questions asked is ONE - using a highly efficient method, the program
'jumps' to the appropriate instruction based on the value of the pressed
key
 Simple Visual Projects involving Sequence and Selection
Simple Visual Projects involving Sequence and Selection
syntax: =df if boolean_exp
then statement
[else statement]
examples:
var x : byte;
begin
x:= 7;
if x > 3
then showmessage('it is bigger')
else showmessage('it is not bigger')
end;
var y : integer;
begin
y:= random(2);
if odd(y)
then showmessage('tails')
else showmessage('heads')
end;
var reply : boolean;
begin
reply := abs(-42) = 42;
if reply
then
begin
showmessage('There''s a bear in there');
showmessage('and a chair as well ")
end
else
begin
showmessage('there are people with games');
showmessage('and stories to tell')
end
end;
It is possible to 'nest' if..then statements in others:
if p
then do something
else if q
then do something else
else do something else still
a side effect to watch out for is a dangling else
if p
then if q
then do something
else do something else
is WRONG - the else connects to the most recently issued if
possible solutions:
if p
then
begin
if q
then do something
end
else do something else
or
if p
then if q
then do something
else
else do something else
IF..THEN..ELSE NESTING - AN EXAMPLE
Problem specification: Write a program that randomly generates
a number in the range 1 - 6, thus simulating the throwing of a die and
outputs the result 'graphically' (ie. 1 = [.], 3 = [.:], 6 = [:::] etc.)
Hints:
randomize : randomly seeds the random number generator
(otherwise you get the same sequence each time the
program is run (usually done in the FORMCREATE)
random(n) : (where n is an integer), produces an INTEGER in the
range 0 .. n-1. So random(3) will produce either a 0, 1
or 2
random(n)+x 'scales up' a random number to fall in the range x..n-1
procedure TForm1.tossclick( Sender: TObject);
{simulates the throwing of a single die, outputting result}
var throw : integer;
begin
throw := random(6)+1;
if throw = 1
then showmessage('[. ]')
else if throw = 2
then showmessage('[: ]')
else if throw = 3
then showmessage('[.: ]')
else if throw = 4
then showmessage('[:: ]')
else if throw = 5
then showmessage('[.::]')
else showmessage('[:::]')
end.
 Binary Branching with IF..THEN
Binary Branching with IF..THEN
THE CASE STATEMENT
In situations where there are a definite number of alternatives, all
of which are known, we use a CASE STATEMENT.
syntax: case identifier of
value1 : statement;
value2 : statement
:
:
[else statement]
end {case}
procedure TForm1.tossclick( Sender: TObject);
{simulates the throwing of a single die, outputting result}
var throw : integer;
begin
throw := random(6)+1;
case throw of
1: showmessage('[. ]');
2: showmessage('[: ]');
3: showmessage('[.: ]');
4: showmessage('[:: ]');
5: showmessage('[.::]');
else showmessage('[:::]')
end {case};
End.
Also legal, lists and sub-ranges of values are valid within a case statement:
eg.
case throw of
1..3 : showmessage('3 or less');
4,6 : showmessage('either 4 or 6')
else showmessage('must be 5')
end; {case throw}
|


